Members-only podcast episode
Adam Tetlow on Mathematics Useful for Understanding Plato

This is a special podcast episode for SHWEP members only
Already a member? Log in here to view this episode
The sixth-century CE Christian Platonist Elias reports that the entrance to Plato’s Academy bore the inscription: ‘Let none who is un-geometric enter’. But, reading scholarly literature on Plato, one could be forgiven for thinking that geometry plays no real role at all in his thought. In this episode we discuss some of the most important numerical and geometrical concepts necessary for a deeper appreciation of dialogues like the Timæus and Republic.
The discussion opens with the basic consideration of what the ancients meant by number, which, it turns out, is in some ways very different from the conceptualisation current in modern mathematics. Number is a principle of reality itself. Ratios – numbers set in relation with each other, but not collapsed into irrational, decimalised single figures – play a major role in this ancient mindset.
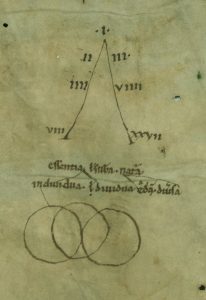
We then move on to a wide-ranging discussion of:
- The theory and practice of musical harmony and the role it plays in Plato’s works,
- The five ‘Platonic solids’,
- The Pythagorean tetraktys and its relationship to the ‘lambda’ figure of Plato’s Timæus,
- And the Golden Section, and its relationship to the Divided Line passage of Plato’s Republic.
The discussion also includes
- A discursus into ancient metrology, debunking the metric system and exploring the fascinating world of ancient measure more generally,
- And discussion of the state of geometry in the modern-day ‘Plato industry’, and the need for scholars of Plato to pick up a compass and straight-edge and get drawing.
Works Discussed in this Episode:
- Critchlow, K., 2007. Time Stands Still: New Light on Megalithic Science. Floris Books, Edinburgh. Critchlow discusses the Platonic solids and their ancient reception.
- Kayser, H. Godwin, J. & Godwin, A. (Ed.), 2006. Textbook of Harmonics. Sacred Science Institute.
- Martineau, J., 2002. A Little Book of Coincidence. Wooden Books, Glastonbury. For the extraordinary harmonic relationship of Venus with the Earth.
- McClain, E., 1978b. The Pythagorean Plato: Prelude to the Song Itself. Nicolas-Hays, York Beach, MN.
- Partch, H., 1979. Genesis of a Music: An Account of a Creative Work, its Roots and its Fulfilments. De Capo. The great Partch’s own account of his music. Technical and philosophical, a very tough read for those daunted by enormous tables of fractions. But check out his music; it’s so hip it’s unbelievable.
Recommended Reading:
- Adam, J., 1985. The Nuptial Number of Plato. Kairos, Wellingborough.
- Critchlow, K., 1976. Islamic Pattern: An Analytical and Cosmological Approach. Thames and Hudson, London.
- Critchlow, K., 2011. The Hidden Geometry of Flowers: Living Rhythms, Form, and Number. Floris Books, Edinburgh.
- Lawlor, R., 2000. Sacred Geometry. Thames and Hudson, London.
- McClain, E., 1978a. The Myth of Invariance: The Origin of the Gods, Mathematics, and Music from the Rg Veda to Plato. Shambhala.
- Michell, J., 1988. The Dimensions of Paradise: The Proportions and Symbolic Numbers of Ancient Cosmology. Thames and Hudson, London.
- Michell, J., 2009. How the World Is Made: The Story of Creation According to Sacred Geometry. Inner Traditions, New York, NY.
- Mountford, J. (1923). ‘The Musical Scales of Plato’s Republic’, Classical Quarterly 17 : 125-36.
- Schneider, M., 1995. A Beginner’s Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and Science. Harper Collins, New York, NY.
- Stewart, M., 2009. Patterns of Eternity: Sacred Geometry and the Starcut Design. Floris Books, Edinburgh.
- Tetlow, A., 2013. Celtic Pattern: Visual Rhythms of the Ancient Mind. Wooden Books, Glastonbury.
- Waterfield, R. (Ed.), 1988. The Theology of Arithmetic. Phanes Press, Grand Rapids, MI.
And for some good practical help with geometric constructions in the old-school way:
- Allen, J., 2007. Drawing Geometry: A Primer of Basic Forms for Artists, Designers and Architects. Floris Books, Edinburgh.
- Sutton, A., 2009. Ruler and Compass. Wooden Books, Glastonbury.


D Graham
June 20, 2019
It would have been helpful to hear more from Adam Tetlow and less from the other person.
Earl Fontainelle
June 22, 2019
Fair comment! The other person has taken note; he is aware that he talks too much sometimes.
Bernie Lewin
September 1, 2019
It helps to remember that ratio was logos and that the importance of golden mean was in ana-logos and continuous generation by logos from a ratio in the linear one. The line divided in this way was thus an analogy of the one with the generator of difference potent within it as per the contradiction in the preface to John that was misunderstood except by Arius. Also important is that sqrt2 was solved by Plato’s time through a continuous emanation (preserved in Theon). Perhaps the irrationals were also infinite emanations of logos!? This explains what Simone weil called the Eudoxian revolution in Pythagorean ism that we now distinguish as platonism. More elementary than number is ratio and this introduced a new idea of geo-numeric emanation by one through its logos. This was the shift from elementary arithmos to elementary logos, where the logos was the first born of all difference (and so the Dyad) already potent in the arche-one or Monad. Leibniz understood this Platonic trasformation of the Pythagorean quest for the essential principle of generation and tried to find the dyad of the (middle) Platonists that he knew tp be more elementary than the Golden Mean, which he thought he found in his image of dyadic creation, but he could not call this generation as ‘by logos’ because the Arian persecution continued in his day.
Earl Fontainelle
September 2, 2019
Bernie,
Heavy. Can you give a reference for Simone Weil? I’d be interested to read her thoughts about the ‘Eudoxian revolution’!
Bernie Lewin
September 2, 2019
Sorry, that was completely over the top but my excuse is that my enthusiasm was arroused by the astute coverage of the topic. Simone Weil is a little esoteric on the “Eudoxian Revolution”, referring to it obliquely a number of times, but the best place to start is with her Intimations of Christianity among the Greeks, especially chapter 11. She and other sources (including Theon of S. – u use his title!) made me understand the Platonic transformation of Pythagoreanism in a whole new way. The shift from arithmos to logos came through the Academy’s part-way solution to the problem of the irrationals, which was all about Eudoxus’s new definition of proportion famously preserved in Euclid bk 5 defn 5, but which is intepreted variously (see eg Heath’s Euclid). For Weil it was that classes of irrationals are in ratio to each other even if not in ratio to 1:2. Eg, all circle geometry is in ratio with itself though 1:pi. Ratio is universal in geometric arithetic. Not so 1:2 arithmos. After Eudoxus the next goal was to find the underlying unity, the absolutely elementary logos that is the first born of the original one and so the principle of all difference, just as per the stoic preface to the gospel of John. Back in Plato the project was more specifically defined: “to find the generative nature of the symmetricals and asymmetricals in relation to one another.” See Laws p.820c. In the academy see Epinomis 990d. Simone Weil opens up a whole new understanding of the monad/logos monad/dyad tradition in middle platonism, in stoicism, through to ante nicene Christianity (and even to Kepler and Leibniz). Look, the convert Weil in her divine madness had the crazy idea of “intimation”, but even if the stoics/Christians had lost the original math source of the mystery of the divine logos, just this desired ratio of all difference might still be the source. If so, it explains what was a revolution in ancient thought that to some extent characterizes Hellenism. The Eudoxan revolution indeed!
Bernie Lewin
September 3, 2019
Clarification:
Eudoxus of Cnidus’ theory of proportion (of “magnitudes in the same logos”) is preserved in Euclid,defn 5, Book 5.
For Simone Weil on its revolutionary importance, a better source is: On Science and Necessity, and the Love of God, OUP, 1968, Ch 1 ‘Classical Science and After’, p. 4 ff (Weil does not seem to use the term “Eudoxan revolution” per se, nor my predictive text misspelling 🙂
Adam Tetlow
February 3, 2021
Interesting comments, most of your points are very astute, but i would argue that the revolution of the Hellenic period was actually a rejection of the harmonic mathematics inherited from Egypt (and many other cultures as early as 10000bc – see Howard Crowhurst’s work on the stones at Carnac in Brittany, John Neal’s work on ancient measure and escpecially Schwaller de Lubicz’s Temple of man chapters 3-7).
The harmonic mathematics of antiquity fully understood the irrational problem but chose to use rational expressions of these values in order to preserve the nature of whole numbers.
The revolution was a reframing that led to mathematics as we know it but has ultimately fuelled materialistic thinking. Hipassus was killed for being an impostor, because he did not understand the initiatory secrets of harmonic mathematics.
Sorry for being so brief, your comments were very in depth and would require a long debate to clarify each point, but sadly i do not have the time for this at the moment.
Emily Stewart
January 21, 2021
a minor correction here, but as someone who has been to (and failed out of) engineering school, we do actually learn to use irrationals! i think it was my college pre-calc class where they first started to emphasize that e.g. √2 is an exact quantity, and if it shows up in a calculation it is preferable to use that instead of reducing it to a decimal, and in every math class i took after that, any ratio or irrational root was to be expressed that way.
once you get into engineering classes where you’re applying the more abstract math to the real world, you *still* use the exact forms during the calculation. at the end of course you’ll collapse it to whatever decimal is appropriate, simply because it’s impossible to cut a beam to exactly √2 feet; it’s always going to be 1.41 or so instead. in my civil engineering classes we generally didn’t bother with precision past a hundredth of a foot, while in my surveying class we went to thousandths. i suspect that mechanical engineering uses more precise tolerances but for human-scale structures you can do a relatively large amount of fudging.
Adam Tetlow
February 3, 2021
Using irrationals in calculation is of course mathematically correct, but by truncating an irrational to a number of decimal places when shaping or measuring materials we are making a rational approximation.
N J Wildberger has some fascinating insights into this area in his YouTube lectures, he gives the example of pi x root2 = pi x root2 as acceptable, yet intellectually dishonest, we would not accept 8 x 11 = 8 x 11, so our mathematics by leaving irrationals unresolved in equation makes an intellectual compromise (even though correct in a computational sense) and departs from the objective reality of number.
Ancient cultures around the world epitomised by Plato used a rational system of harmonic intervals to avoid making this compromise.